hemos soñado el mundo. Lo hemos soñado resistente,
misterioso, visible, ubicuo en el espacio y firme en el
tiempo; pero hemos consentido en su arquitectura tenues y
eternos interstícios de sinrazón para saber que es falso.
J. L. Borges, Avatares de la tortuga, in Discusión, pag. 136,
[Obras completas, Vol. I, EMECÉ, Buenos Aires ]
O meu último post conseguiu um dos seus objectivos, que era o de provocar uma controvérsia. Não conseguiu o objectivo principal que era o de contribuir, pouco que fosse, para desmistificar os tabus da MQ. Alguns dos comentários que suscitou levaram, com certeza, muitas pessoas a fugir da MQ a sete pés. Agradeço aos que fizeram comentários positivos e aos que fizeram críticas construtivas. Não esperava despertar os obstinados "trolls" de serviço, escondidos, de rabo de fora. Quem conhece a língua de Aquilino e de Torga, e leu o meu texto com atenção, percebeu o que pretendia. O bom observador também terá notado o ponto de interrogação na figura do meu gato (de Schrödinger).
Para atingir os objectivos que me propus, de introduzir as regras (postulados) da MQ e deles retirar alguns dos conceitos fundamentais, não preciso de condições de quantização envolvendo infinitos, nem de análise de Fourier, nem de teoria de grupos. E creio que "vectores" e "números complexos" ainda são do programa do ensino secundário.
Certas experiências são suficientemente simples para poderem ser feitas num laboratório rudimentar. A título de exemplo, poderiam introduzir-se os conceitos de estado e de sobreposição de estados, para fotões, usando apenas um laser (dos que se compram na loja dos chineses) e algumas folhas de plástico polaroid. Podem encontrar-se kits na internet por cerca de 30 dólares.
Tendo em atenção uma das críticas construtivas vou tentar ilustrar as minhas regras do jogo com alguns exemplos.
Transcrevo a 1ª regra: Num dado instante o estado de um sistema físico é especificado por um elemento (pode ser vector ortonormado) chamado "estado", que satisfaz as regras de uma álgebra linear, e é representado por um símbolo x. Quando observo uma moeda que atirei ao ar e caiu com a face caras para cima, digo que o "estado" da moeda é "caras" ou x. Classicamente, a moeda, ao cair, só pode assumir um dos dois estados x e y. Em MQ, deve considerar-se ainda um estado intermédio, u, que é a soma ou sobreposição dos dois estados e se representa por u = ax + by, em que a e b são números. Isso é matematicamente correcto, porque numa álgebra linear, qualquer dos seus elementos pode sempre ser escrito como uma soma de outros (é o caso dos vectores).
Exemplos: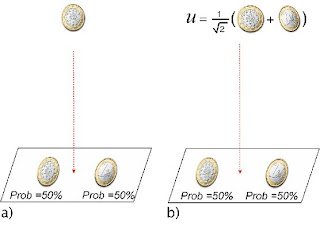
Suponhamos que lanço uma moeda ao ar, a qual depois cai sobre uma mesa.
i) Na perspectiva da física clássica e da teoria de probabilidades, a probabilidade de cair caras é 50% e a de cair coroas também de 50%. A situação é ilustrada na figura, na qual, em cima, se mostra apenas uma das faces da moeda, (podendo ser a outra). Se tirasse uma fotografia instantânea à moeda quando ela estivesse no ar, teria 50% de probabilidade de ver caras e 50% de ver coroas.
ii) Admitamos que, para efeitos do jogo, (que pretende ser apenas uma metáfora da MQ, e não uma analogia) quando atiro a moeda ao ar, há alguns instantes em que a moeda (ou os deuses ou Deus) ainda não decidiu para que lado cairia. Durante esses instantes assume-se que a moeda está num estado não definido do tipo u = ax + by, mais concretamente u = 0.7071 x + 0.7071 y; em que x (caras) e y (coroas) são os dois únicos estados possíveis (em que a moeda pode cair) e ignoro todos os outros atributos da moeda. Qual é a probabilidade de, num único lançamento, observar o resultado caras?
Segundo a 1ª regra, a probabilidade de cair caras é a2 = 0.70712 ou seja 0.500 (i.e., 50%). Identicamente a probabilidade de obter coroas é b2 = 0.70712 (0.500 ou 50%).
Naturalmente que a soma é 1, na medida em que a moeda tem de cair numa das duas posições (excluindo, por agora, a possibilidade de cair em pé). Essa condição que não foi explicitada nas regras, é uma consequência da lógica do problema, e está formalmente implícita quando digo que os elementos da álgebra (p.ex., vectores) são ortonormados.
Suponhamos agora que a moeda era defeituosa e que teria maior tendência para cair para o lado coroas. Tal situação poderia ser descrita por um elemento como, por exemplo, u = 0.500 x + 0.866 y, o que daria as probabilidades de cair caras ou coroas de 25% e 75% respectivamente.
Admitamos ainda que a moeda poderia cair em pé. Então deveria considerar-se um terceiro estado possível, por exemplo, w (em pé). Se antes de cair, a moeda fosse descrita pelo estado u = 0.7068 x + 0.7068 y + 0.030 w, então as probabilidades de cair respectivamente caras, coroas e em pé, seriam aproximadamente 0.70682 = 0.4996 (49.96%), 0.70682 = 0.4996 (49.96%), e 0.0302 = 0.0009 (aproximadamente 1 por mil). As mesmas condições de a soma de todas as probabilidades ser 1, são aplicadas.
Como se vê, neste caso, o resultado da MQ é idêntico ao da mecânica clássica com o cálculo de probabilidades clássico. Não temos até agora maneira de distinguir se o comportamento é clássico ou quântico. Mas podemos modificar um pouco a experiência imaginária (thought experiment) de modo a distinguir entre uma situação quântica e a correspondente situação clássica.
Para não sobrecarregar o blog, convido as pessoas interessadas a fazer o download do texto completo deste exercício que pode ser encontrado aqui.


2 comentários:
Um troll feio e sujo, refere que misteriosamente o blog ficou fechado a comentários não identificados. Pois bem, aqui vai um comentário construtivo: o Luís Alcacer deveria ir aprender a MQ que ignora. Ele deve pensar que a MQ são só uns exercícios mal explicados e desprovidos de contexto.
O leitor geral não quer apender exercícios infantis que nunca vai utilizar, mas sim os fundamentos da MQ, infelizmente isso não é o forte do Luís, que nada percebe da essência da questão.
Sugiro que leiam os comentários do post anterior.
E as tretas continuam. Se a MQ é assim tão mais simples em termos matemáticos do que a Mecânica Clássica então não deve ter problemas em resolver o problema que indiquei no seu primeiro post:
«Se acha realmente que a Matemática associada à MQ é mais simples do que a envolvida na Mecânica Clássica desafio-o a resolver aqui a descrição da queda de um grave em mecânica quântica e depois em termos clássicos. Depois disso falamos.»
Afinal, a queda de graves é dos problemas mais simples em Mecânica clássica.
Não tenho ilusões. Não o resolveu há ano e meio, não deverá ser agora que resolve.
Enviar um comentário